Essential Math Weblog Thoughts on math for games

So at the end of my GDC 2015 presentation “How to Draw an Anti-Aliased Ellipse” I mentioned that you could extend the same techniques to signed distance fields (SDFs), in particular for text. However, some details might be helpful. Because SDFs encode distance directly, the approach is slightly different than for an implicit field like ellipses. I also made a grandiose statement that you should use the shaders in Skia because all the others don’t work properly. After prepping this post, I realized that was half right — the case that we see 99% of the time in Chrome is correct, but the case that you might see in a 3D world — e.g., a decal on a wall — is not. I’ll talk about a better way to handle that in Part Two.

So first, go look at the presentation linked above, just as a quick review. I’ll wait.

We’ll start discussing SDFs by generating a shader that renders one without worrying about transformations. To review: a signed distance field is just a texture that stores distance values rather than color values. Negative distances mean we’re inside the shape; positive means we’re outside; zero means we’re right on the border. We’re going to render our texture so that one texel is the same scale as our pixels. So if we have a 32 x 24 glyph, we’ll render it with a 32 x 24 quad in screen space. I’m not going to get into how to encode the distance — you could use an 8-bit fixed point value and decode in the shader (as we do in Skia), or use a half or single precision float texture (as we might do in Skia someday).

We’d like a shader that approximates pixel coverage based on the distance to the edge. If the distance is 0 (i.e., the shape hits the pixel center exactly) then a coverage of 50% seems like a reasonable approximation. But what about the edge cases? The maximum distance from the pixel center to the outside of the pixel is the distance to one of the corners or . So one possibility is to map or less to be 100% coverage, and or more to be 0% coverage, and blend the values between. The following fragment or pixel shader code will handle that:

float distance = texture_lookup(uv);
float afwidth = 0.7071;
float coverage = smoothstep(afwidth, -afwidth, distance);

And that’s it. Again, this assumes that both: a) the quad we render with is the same size as the distance field’s rectangle in the texture, and b) that we’re not applying any scaling or perspective to the quad (translate and rotation won’t change the texel-to-pixel scale).

Another possibility for afwidth is to use 0.5, the distance to one of the edges of the pixel; this will give you a sharper edge. Both are only an approximation to the coverage, so it’s hard to say that one is more correct than the other — it’s really a matter of taste of how sharp or blurry you want your edge to be. It’s also possible to use a linear ramp function rather than smoothstep(). Again, we’re only approximating coverage so it’s hard to say which to choose. The ramp may be faster to compute, but smoothstep() may look better. In my early tests 0.7071 and smoothstep() gave better results, but a lot has changed since then — I may go back and revisit it to try to some other values.

Anyhow, this basic shader is not terribly interesting or useful, so let’s apply a transformation to our quad and adjust the shader to handle that. We’ll make things easy by first only considering uniform scale. So for the 2D case, the transformation matrix is:

Let’s apply this to a simple distance field, say a circle (sort of pointless since the presentation shows how to render circles directly, but what the hey). Figure a) shows the circle and two isodistance contours, inside and outside; Figure b) shows the situation after we scale.

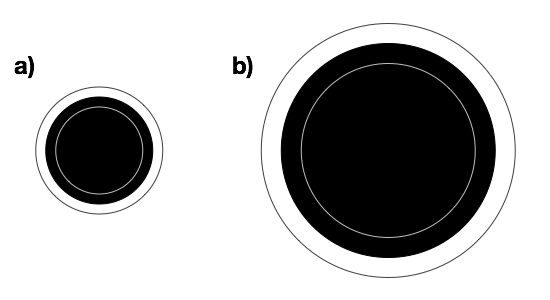
If the outer ring represents, say, a distance of 1 from the circle, then we’d expect it to remain a distance of 1 away from the edge. But it’s now a distance of 2 away. This is what will happen when we scale up our quad: we’ll do a texture lookup and it’ll give us a distance of 1, but it really should be giving a distance of 2. The end result is that we’ll blur our antialiased edge over four pixels instead of just two.

There are a couple of possibilities to correct this. One is to scale the distance from the texture by . The other is to scale afwidth by . In this simple example it’s six of one, half dozen of another, but we’ll go with scaling afwidth. So then our fragment or pixel shader code becomes

float distance = texture_lookup(uv);
float afwidth = 0.7071*recip_scale; // divide by scale
float coverage = smoothstep(afwidth, -afwidth, distance);

So where do we get the reciprocal scale? Since the transform is affine, one way is to pass it in as a uniform or shader constant. Another is to compute it in the vertex shader from the transform matrix (which you probably are already using in the vertex shader) and pass it down as an input to the fragment/pixel shader. There is a third way, which is to use the dFdx() operator — but I’ll talk about that later.

So this handles uniform scale fine, which is okay for the common cases in web pages, but not so good for 3D worlds. We’d really like a general shader which can handle any transformation, or even a quad of a different size. And I’ll cover that next time as well.